Introduction to DG Jargon
When I first began studying discontinuous Galerkin (DG) methods, I found myself confused on some of the terminology being used. I have collected some jargon and will be continuously updated. Enjoy!
- Mesh: The mesh is the discretization of the computational domain. The mesh is usually composed of triangles and/or quadrilaterals (quads) in 2D and tetraherals (tets) and/or hexahedrals (hexes) in 3D. One of the reasons why we push into the DG world is to be able to have unstructured meshes. A structured mesh is usually made up of quads or hexes and ends up looking like a Cartesian grid. In the case of unstructured meshes the most visually obvious property that there might be different sized and shaped elements. Unstructured meshes are great when complex geometry is involved such as airfoils, airplanes, wind turbines, and other objects. Unstructured meshes are more formally defined based on the valence the vertices of the elements. The average valence for triangles is 6 and the average valence for quads is 4. For unstructured meshes, then valence of an vertex may be larger or smaller than the average valence. This lecture gives a good description of unstructured meshes. I also tend to use Gmsh for generating meshes.
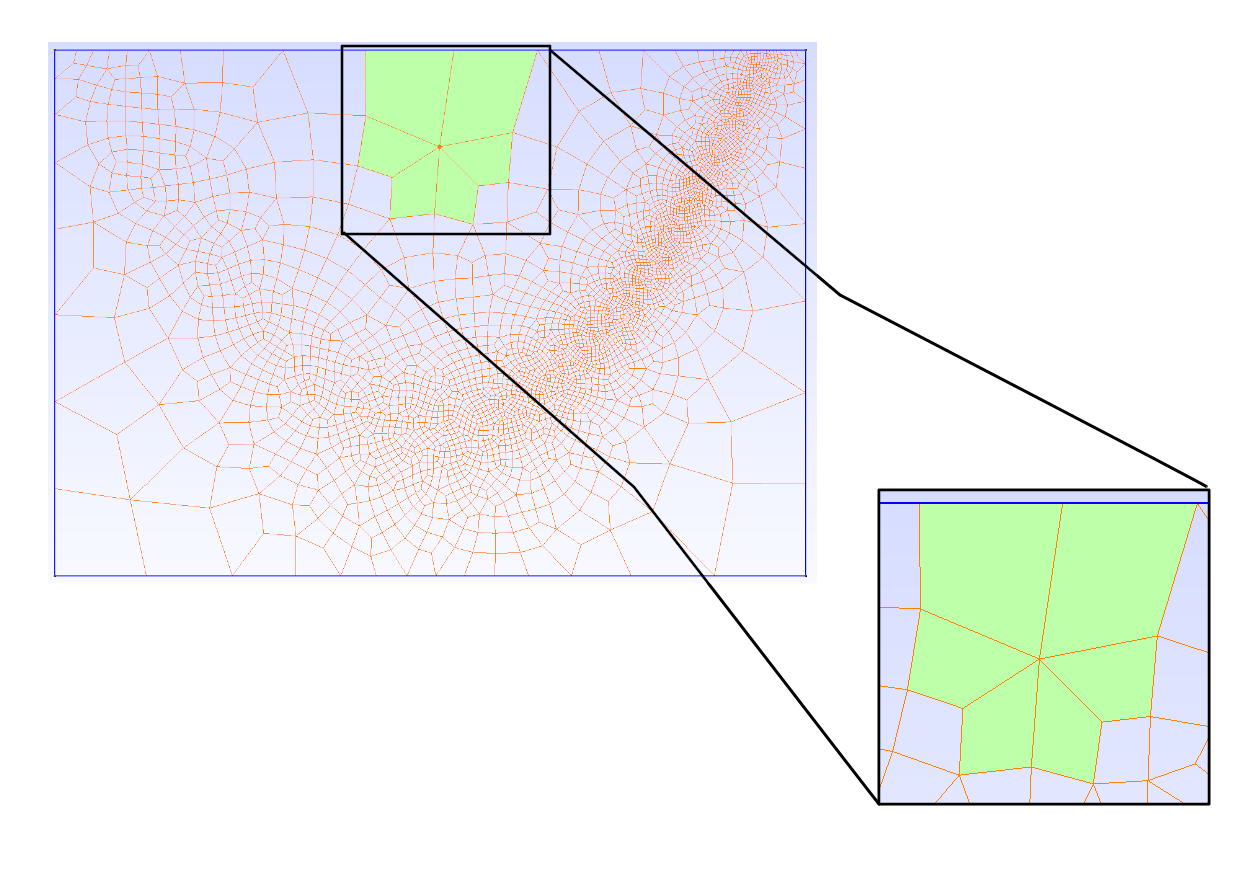 Figure 1 - This is an example of a unstructured quad mesh. The green elements are of interest since they show that a vertex can have a valence of more than 4.
Figure 1 - This is an example of a unstructured quad mesh. The green elements are of interest since they show that a vertex can have a valence of more than 4.
- Element: The most popular elements are triangles/tets and quads/hexes. Each element houses the approximation to the solution that is defined . In the case of DG, then the solution is local to the element and mostly independent of the rest of the mesh with the exception of neighboring elements. The neighboring elements are used to compute the numerical flux and discretizations of higher-order operators.
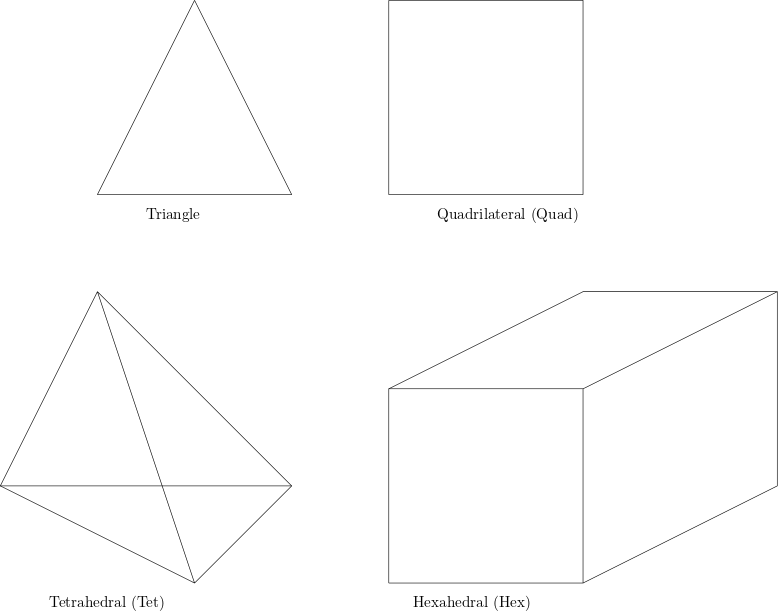
Figure 2 - Here we can see the different type of elements for two dimension (triangles and quads) and for three dimensions (tets and hexes).
-
Nodal Points (nodes): Within each element, we have a set of nodes that are used to approximate the solution. In my experience, nodes are usually defined using Gauss-Lobatto quadrature rule. The number of nodes is $p+1$ where $p$ is the order of the approximating polynomial. The basis functions are defined on these nodal points.
-
Quadrature Points: The quadrature points are also generated using Gauss-Lobatto rule. The number of quadrature points is one of the many tunable knobs of DG methods. If we let the number of nodes be equal to the number of quadrature points, i.e. $n_n = n_q$, then we have the popular nodal DG method. In this case you will always under-integrate but have a less quadrature points. However, we know that the quadrature is exact for polynomials of $2n-3$. A popular choice of quadrature points is $n_q = p+1$ which will integrate a polynomial of order $2p-1$ exactly. However, if you want to be handle quadratic nonlinearities in the flux function then $n_q = \frac{3}{2}(p+1)$ will be a perfect choice.
-
Quick Recap…: The last four keywords we discussed are pretty important and are a basis (hehe pun intended), so let’s see how they fit together. For every mesh, we have many elements. For line DG, we use quads and hexes. Within every element, we have a set of nodal points and a set of quadrature points. The nodal and quadrature points do not need to be the same but can be. So here is a figure describing how the different elements are connected…

Figure 3 -Two-dimensional Cartesian mesh with 36 elements. Each element then has 9 nodal points (3 nodal points per direction) and 25 quadrature points (5 quadrature points in each direction).
-
Modal Solution: The modal solution can be thought of as a sum of multiple waves with $p+1$ distinct frequencies and amplitudes. In other words it is given by $u(x,t) = \sum_{i = 0}^{p} \tilde{u}(t) \phi_i(x)$. The monomial expansion is one example of a modal representation and it is given by $\phi_i(x) = x^{i}$.
-
Nodal Solution: The nodal soution is defined at the Gauss-Lobatto nodes. The nodal expansion can be written as $u(x,t) = \sum_{i = 0}^{p} u(x_i,t) \ell_i(x)$ where $\ell$ is the Lagrange polynomial.
-
Nodal vs Modal?: Using the standard Vandermonde matrix then we can switch between a nodal and modal representations, $u = V\tilde{u}$. There is a pros and cons to each representation. However, modal expansion might not necessarily lead to an orthogonal basis, especially for high-orders. Check this link out for a brief discussion.
Last updated: 26 May 2021